Screened Waves
a jigsaw puzzle-like basis set for 1-particle wavefunctions
Dimitar Pashov, KCL
IIIDQS, 16 May 2019, STFC Daresbury
Idea
Construct a set of functions which almost solve the 1-particle Schrödinger/Dirac equation for real potentials
without spending effort equivalent to or grater than actually solving it.
- Without global matrix operations: multiplication, inversion, diagonalisation, decompositions, etc...
- Without global energy scan and functions reconstructions
The function set shall
- preserve the rigour and accuracy of augmented methods
- be mimimal, reasonably complete and not overcomplete
- be reasonably short ranged (system dependent), allowing scalable integration
- take advantage of low expansion cutoffs of the PAW scheme (described in Mark's intro to LMTO talk).
![]()
![]()
![]()
s-type function (interactve isosurface model)
QSGW Si bandstructure
![]()
![]()
Short deviation to explain yesterday's unfortunate confusion on the LiF example
blm --gw --nkgw=5 --nk=8 --nit=20 --gmax=9.8 --ctrl=ctrl init.lif
interpolating 8×8×8 mesh from 5×5×5 sigma file on a tiny system, potentially dangerous (as we saw yesterday with Brian), terribly false gap of 2.44 eV, parallels with 2×2×2 Si bands picture (unscreened case):
![]()
vs
blm --gw --nkgw=5 --nk=5 --nit=20 --gmax=9.8 --ctrl=ctrl init.lif
interpolating 5×5×5 mesh from 5×5×5 sigma more reliable because points match (bar the Γ point, which always gets a special treatment): bandgap: 16.65 eV
Truncated QSGW NiO band gap
![]()
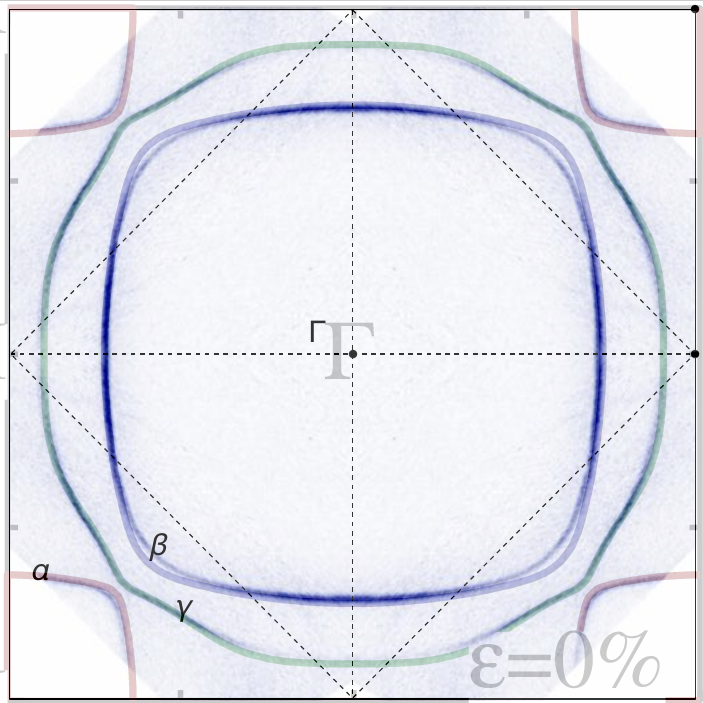
Strontium Ruthenate Fermi surface (8×8×8 mesh)
experiment, screened (overlay) and unscreened basis
![]()
![]()
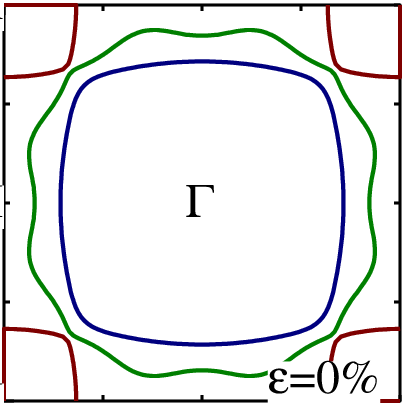
Strontium Ruthenate 6×6×6 screened basis
![]()
Screened LMTO in a coconutshell
$H$: $h.Y$; $J$: $j.Y$; $Y$: spherical harmonics; $I$: identity (sometimes product of Kronecker deltas)
$H_{RLR'L'}$ : The $L'$ component of a function $H_L$ centered on site $R$ evaluated at site $R'$.
\[
H_{RLR'L'} = H_{L} I_{RLR'L'} + S_{RLR'L'} J_{L'} . (1-I_{RR'})
\]
(in smooth H case there is additional short ranged $P_{kL}$ expansion of $H^{sm}-H$ which is ignored here for clarity)
Here $S_{RLR'L'}$ is an expansion coefficient such that $H_{RL(r)} = \sum_{L'} S_{RLR'L'} J_{L'R}$
Let's concretise for sphere surfaces only and rescale by $1/H_{L'}$ rather than $1/H_{L}$ to preserve the original symmetry of $J$ $\left(\right.$now $\left. J/H\right)$, $H_{L} I_{RLR'L'} / H_{L'} == H_{L} I_{RLR'L'} / H_{L} == I_{RLR'L'}$ for spheres of the same size anyway.
\[
H_{RLR'L'}/H_{L'} = I_{RLR'L'} + S_{RLR'L'} J_{L'}/H_{L'} . (1-I_{RR'})
\]
Let's shorten $J_{L}/H_{L}$ to just $\alpha_{L}$, it is a diagonal in matrix form. With $\mathrm{H} \equiv H_{RLR'L'}/H_{L'}$ and other appropriate aliasing:
\[
\mathrm{H} = \mathrm{I} + \mathrm{S} \alpha
\]
Now request functions $E_{RL}$ made of combinations of H functions such that they evaluate to unit on their own $R$ centered spheres but vanish at all other spheres (i.e. I_{RLR'L'}). The combination coefficients $B$ are to be found.
\[
E_{RLR'L'} = H_{L} δ_{RR'} δ_{LL'} = \sum_{R''L''} B_{RLR''L''} H_{R''L''R'L'}
\]
to avoid messy indices let's alias $\mathrm{E} \equiv E_{RLR'L'}/H_{L'} \equiv \mathrm{I}$, then:
\[
\mathrm{E} = \mathrm{B} \mathrm{H}; \quad \mathrm{B} = \mathrm{E} \mathrm{H^{-1}} = (\mathrm{I} + \mathrm{S} \alpha)^{-1} = a^{-1} (a^{-1} + \mathrm{S})^{-1}
\]
We do have kinks on the sphere boundaries due to the augmentation functions mathing the value (and curvature) only.
\begin{align}
& K_{1,RLR'L'} = & dE_{1,RLR'L'} - & d\phi_{1,RLR'L'} \\
& K_{2,RLR'L'} = & dE_{2,RLR'L'} - & d\phi_{2,RLR'L'} \\
& : : & & : \\
& K_{n,RLR'L'} = & dE_{n,RLR'L'} - & d\phi_{n,RLR'L'}
\end{align}
these can be straightened out by interpolating to 0 kink matrix using functions at 2 or more energies. Example with Lagrange weights:
\[
F = \sum_{e=1}^n \left( \prod_{k=1;k/=e}^n K_k . (K_k - K_e)^{-1} \right) E_e
\]
The same can also be derived (with more difficulty) from the Vandermonde matrix:
\begin{align}
F = (I\, 0\, 0) & (K_1^0 K_1^1 ... K_1^n)^{-1} & E_1 \\
& (K_2^0 K_2^1 ... K_2^n) & E_2 \\
& : : ::: : & : \\
& (K_n^0 K_n^1 ... K_n^n) & E_n \\
\end{align}
For the simple case of 2 energies:
\[
F = K_2 (K_2 - K_1)^{-1} E_1 - K_1 (K_2 - K_1)^{-1} E_2
\]
adding more linearisation energies sharpens the window of accuracy, (improves significntly between the energies and worsens as much outside of it).
Step by step construction with a toy model
![]()
fairly realistic (not a muffin tin) yet simple analytic solution available for reference
Bare (un smoothened) Hankel basis vs analytic solution
![]()
Screening
note behaviour on sphere boundaries
![]()
Augmentation (kinked waves)
Bare (un smoothened) Hankel basis vs analytic solution
![]()
![]() bare H need 0 interstitial volume (not the case here) to be effective on real (not flat) potentials.
bare H need 0 interstitial volume (not the case here) to be effective on real (not flat) potentials.
Smooth Hankel basis vs analytic solution
![]()
Screening
same behaviour on sphere boundaries
![]()
Augmentation (kinked waves)
Smooth Hankel basis vs analytic solution
![]()
![]() smoothing helps on real potetials (compared with bare H which are only exact for flat potential)
smoothing helps on real potetials (compared with bare H which are only exact for flat potential)
Smooth Hankel basis (k.e. match) vs analytic solution
![]()
Screening
note continuity of curvature across sphere boundaries
![]()
Augmentation (kinked waves)
Smooth Hankel basis (k.e. match) vs analytic solution
![]()
![]() functional solution close to perfect
functional solution close to perfect