Magnetism in lmf
LDA description of ErAs
Erbium arsenide has the rock salt structure; the 11 Er electrons take up localised, atomic-like states and form a moment of (7 “up”, 4 “down”). The LDA description, failing to distinguish between the occupied and unoccupied minority f-states, places these minority states at , giving a metallic description. LDA+U correctly splits the occupied and unoccupied states, moving the f-states away from the Fermi-level and restoring the observed semi-metallic behaviour.
1. Converged LDA calculation and density of states
cp /home/vol05/tmp15/eras_icsd_43644.cif .
cif2cell eras_icsd_43644.cif >out
cif2init out
mv init init.eras
blm eras
cp actrl.eras ctrl.eras
vi ctrl.eras
Edit the ctrl file to prepare for a magnetic calculation:
% const nit=50
% const so=0 nsp=2 # spin polarisation
% const lxcf=1 lxcf1=0 lxcf2=0 # use CA not BH
% const nkabc=0 gmax=0 beta=.1 # small mixing for tricky system
ATOM=Er Z= 68 R= 2.846545 LMX=3 LMXA=6 MMOM=0 0 0 3
Run the atom solver lmfa, and update the gmax token with the recommended value (9.4 a.u.). Set nkabc=8, a reasonable mesh here.
lmfa --usebasp eras | tee log_lmfa
grep GMAX log_lmfa
vi ctrl.eras
mpirun -np 24 lmf eras | tee log_lmf-lda
The calculation converges to a total moment somewhat less than 3. Notice that the total moment is also echoed in the save.eras file. states/Ryd.
BZWTS : --- Tetrahedron Integration ---
Est E_f Window Tolerance DOS(E_f)
-0.041188 -0.041424 -0.040460 0.000964 752.425776
-0.041241 -0.041251 -0.041241 0.000010 **********
-0.041241 -0.041241 -0.041241 0.000000 **********
BZINTS: Fermi energy: -0.041241; 25.000000 electrons; D(Ef): 1025.571
Sum occ. bands: -14.1291269 incl. Bloechl correction: -0.000399
Mag. moment: 2.721098
Saved qp weights ...
mkrout: Qtrue sm,loc local true mm smooth mm local mm
1 18.434947 4.536714 13.898233 2.623196 0.114373 2.508824
contr. to mm extrapolated for r>rmt: 0.050070 est. true mm = 2.673266
2 4.113469 4.620245 -0.506777 0.059428 0.057311 0.002117
contr. to mm extrapolated for r>rmt: 0.082335 est. true mm = 0.141763
To plot the density of states:
mpirun -np 24 lmf --quit=dos --dos~npts=2001~window=-1,1 eras |tee log_dos
echo 25 20 -12 12 | pldos -esclxy=13.6057 -ef=0 -fplot -lst=1 -lst2 dos.eras
fplot -f plot.dos
ps2pdf fplot.ps eras_dos_lda.pdf
The arguments to pldos limit the scale to 25 states/eV , sets the figure size to 20cm and plots between -12 and 12 eV. Note “-lst2” which includes the second spin channel with opposite sign.
Of course the system is ferromagnetic by construction because there is only one Er site.
2. LDA+U calculation and density of states
Update the ctrl file by adding these tokens for the LDA+U method:
SYMGRP R4Z MZ
ITER
UMIX=0.5
SPEC
ATOM=Er Z= 68 R= 2.846545 LMX=3 LMXA=6 MMOM=0 0 0 3
IDU= 0 0 0 12
UH= 0 0 0 {8.0/12.6057}
JH= 0 0 0 {0.5/12.6057}
Notes:
- IDU=0,1,2 for no +U, AMF or FLL double counting corrections – a list over
- IDU+=10 flags the inclusion of as well as
- UH,JH values of U,J in Ryd
- UMIX stabilises the calculation (mixing beta for the density matrix)
- remove symmetry operations which rotate
SYMGRP find SOC=1
(find symmetry operations for LDA+U or SO.)
Initial occupations can be specified in a simple way in the occnum.eras file:
% real
1 1 1 1 1 1 1
0 0 0 1 1 1 1
Notes:
- without %real, complex spherical harmonics are understood
- ordered -l:l for majority, minority spins
- add blocks in sequence for more than one +U set
Run lmf as usual, repeat as required.
sudmtu: no file dmats ... read (diagonal) density-matrix from occnum file
occ numbers, site 1 l=3: 1 1 1 1 1 1 1 (spin 1) 0 0 0 1 1 1 1 (spin 2)
sudmtu: RMS change in dmats from symmetrization = 0.071429
(warning) RMS change unexpectely large
lmf prints the new density matrices at every iteration and updates the dmats.eras file (which is human-readable). Ultimately, lmf reports the converged results:
LDA+U total energy ...
ldau: version = 2 iblu = 1
vldau: Eldau = 20.860170 Edc = 20.330652 Eorb = 0.529517
eks = -30673.344939 e[U] = 0.529517 Etot(LDA+U) = -30672.815422
LDA+U update density matrix ...
RMS diff in dens mat(1.22e-4) > tolu (0) Linear mix with beta=0.5
RMS change in vorb from symmetrization = 0.000003
Mixed dmats l=3 site 1 spin 1, spherical harmonics
0.78743 0.00000 0.00016 0.00000 0.00000 0.00000 0.00000
0.00000 0.78619 0.00000 0.00000 0.00000 -0.00008 0.00000
0.00016 0.00000 0.79146 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.78855 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.79186 0.00000 -0.00016
0.00000 -0.00008 0.00000 0.00000 0.00000 0.78917 0.00000
0.00000 0.00000 0.00000 0.00000 -0.00016 0.00000 0.78971
0.00000 0.00000 0.00000 0.00000 -0.00001 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.00000 -0.00002 0.00000
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00001
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00001 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00002 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 -0.00001 0.00000 0.00000 0.00000 0.00000
Mixed dmats l=3 site 1 spin 2, spherical harmonics
0.01420 0.00000 0.00094 0.00000 0.00367 0.00000 0.00000
0.00000 0.00464 0.00000 0.00000 0.00000 -0.00439 0.00000
0.00094 0.00000 0.01646 0.00000 0.00000 0.00000 0.00367
0.00000 0.00000 0.00000 0.76925 0.00000 0.00000 0.00000
0.00367 0.00000 0.00000 0.00000 0.77357 0.00000 -0.00094
0.00000 -0.00439 0.00000 0.00000 0.00000 0.76978 0.00000
0.00000 0.00000 0.00367 0.00000 -0.00094 0.00000 0.76992
0.00000 0.00000 -0.00022 0.00000 -0.00002 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.00000 0.00002 0.00000
0.00022 0.00000 0.00000 0.00000 0.00000 0.00000 0.00002
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00002 0.00000 0.00000 0.00000 0.00000 0.00000 -0.00022
0.00000 -0.00002 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 -0.00002 0.00000 0.00022 0.00000 0.00000
and,
IORBTM: orbital moments :
site spec spin Moment decomposed by l ...
1 Er 1 0.000000 -0.012462 -0.031719 0.008341 0.000126 0.000034 0.000013
1 Er 2 0.000000 0.012755 0.028980 5.917473 -0.000126 -0.000039 -0.000011
1 L+ - L- 5.923366
2 As 1 0.000000 -0.020485 0.001009 -0.000002 0.000000 0.000000 0.000000
2 As 2 0.000000 0.018723 -0.001704 -0.000234 0.000000 0.000000 0.000000
2 L+ - L- -0.002693
BZWTS : --- Tetrahedron Integration ---
Est E_f Window Tolerance DOS(E_f)
-0.003115 -0.003141 -0.002077 0.001064 2.351381
-0.003115 -0.003120 -0.003109 0.000011 2.347617
-0.003115 -0.003115 -0.003115 0.000000 2.347612
BZINTS: Fermi energy: -0.003115; 25.000000 electrons; D(Ef): 2.348
Sum occ. bands: -19.5837013 incl. Bloechl correction: -0.000834
Mag. moment: 2.995678
Saved qp weights ...
mkrout: Qtrue sm,loc local true mm smooth mm local mm
1 18.322237 5.281827 13.040410 3.005389 0.176453 2.828936
mag true -0.000054 0.000037 3.005389 smooth -0.000143 -0.000268 0.176452
contr. to mm extrapolated for r>rmt: 0.007134 est. true mm = 3.012523
2 4.148275 4.658113 -0.509838 0.017586 0.021715 -0.004129
mag true -0.000104 -0.000233 -0.017584 smooth -0.000092 -0.000155 -0.021714
contr. to mm extrapolated for r>rmt: -0.001736 est. true mm = 0.015850
Corresponding to the occnum.eras, we arrived at the configuration with maximum orbital moment. Other configurations, with different energies, can be reached from different starting configurations (try!).
Both the total and Er local moment are close to 3, and is sensible.
mpirun -np 24 lmf --quit=dos --dos~npts=2001~window=-1,1 eras |tee log_dos
echo 25 20 -12 12 | pldos -esclxy=13.6057 -ef=0 -fplot -lst=1 -lst2 dos.eras
fplot -f plot.dos
ps2pdf fplot.ps eras_dos_ldau.pdf
LDA+U is quite effective here.
3. Adding spin-orbit and plotting the band structure
Including spin-orbit is achieved by setting HAM_SO greater than zero. SO=1 adds the full to the Hamiltonian. SO=2,3 are methods, based on , for keeping the Hamiltonian spin-diagonal as is necessary for the GW codes.
% const so=1 nsp=2
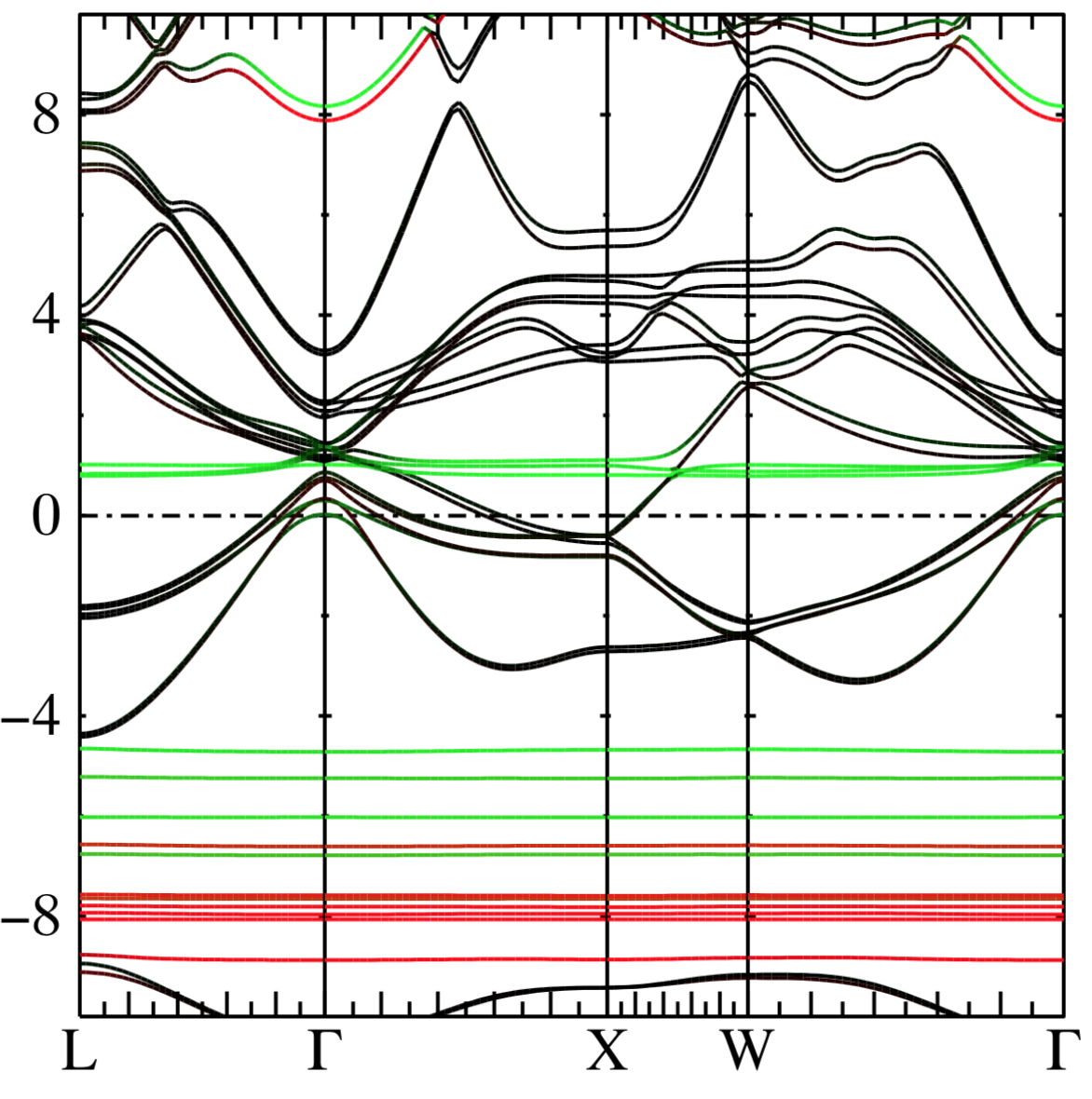
Because the spin channels are now mixed, the plotting spin-up and -down bands doesn’t make sense. Instead it is effective to colour the weights by the spin: here we highlight the Er majority f-states in red, minority in green. A suitable -path might be (copy into qp.eras):
41 .5 .5 .5 0 0 0 L to Gamma (Lambda)
41 0 0 0 1 0 0 Gamma to X (Delta)
21 1 0 0 1 .5 0 X to W (Z)
41 1 .5 0 0 0 0 W to Gamma (no name?)
0 0 0 0 0 0 0
then we proceed as usual, noting that the spin-down basis functions are offset by 48 from the spin-up.
lmf --pr61 --quit=ham eras
lmf --band~col=10:16,26:32~col2=48+10:48+16,48+26:48+32 eras
echo -10 10 10 10 | plbnds -fplot -ef0 -scl=12.6057 -lbl=L,G,X,W,G -lt=1,col=0,0,0,colw=1,0,0,colw2=0,1,0 bnds.eras
fplot -f plot.plbnds
ps2pdf fplot.ps eras_bands_ldaso.pdf