The Questaal Suite

Table of Contents

• Introduction
• Comparing ab initio formalisms
  • One body potentials
  • Many body approaches
  • Relative merits of different approximations
• Executable codes in the Questaal suite
  • Input for Questaal codes
  • Utilities to prepare input
  • One-body Electronic Structure Codes
  • Greens function implementations
  • Supporting or Postprocessing codes
• Other Resources

Introduction

The Questaal suite consists of a collection of electronic structure codes for crystals, based on the local-density approximation (LDA), with some extensions, to density functional theory. An overview of Questaal’s density-functional implementation is presented here, but Questaal’s primary distinguishing feature is the extensions to GW, particularly Quasiparticle Self-Consistent GW approximation (QSGW). The DFT/QSGW codes also have an interface to two Dynamical Mean Field theory packages (DMFT), making it possible to combine QSGW (or DFT) with DMFT. This news highlight outlines some of Questaal’s unique features, in particular it ability to carry out QSGW calculations, and combine it with DMFT and extensions. See also this psi-k highlight.

In addition to the main density-functional (DFT) code, a suite of three density-functional codes based on the Atomic Spheres Approximation are also part of Questaal. These are more approximate than full-potential methods, but have other kinds of functionality. The crystal Green’s function code has the ability to calculate magnetic exchange interactions, and implementation of the coherent potential approximation which allows both finite temperature and lattice disorder, and a layer Green’s function method with an implementation of Landauer-Buttiker transport.

Most of the programs in the Questaal suite descended from the LMTO formalism developed in the 1980’s by O.K. Andersen’s group in Stuttgart. Questaal codes have been written mainly by M. van Schilfgaarde, though many people have made important contributions. To download the package follow this link.

This paper is the main reference for the Questaal package:

Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2019). https://doi.org/10.1016/j.cpc.2019.107065

If you disseminate results generated by Questaal codes for any purpose, please refer to this paper.

Comparing ab initio formalisms

Electronic structure methods must start from a hamiltonian or a Green’s function. Model hamiltonians such as the Hubbard model, the empirical pseudopotential method or tight-binding models such as tbe implements are parameterized, e.g. in terms of Slater-Koster matrix elements.

One body potentials

Electronic structure methods must start from a hamiltonian or a Green’s function. Model hamiltonians such as the tight-binding code tbe are parameterized, e.g. in terms of Slater-Koster matrix elements. By contrast ab initio hamiltonians have a potential, which is constructed from the theory itself. What form this potential takes depends on the approximation made. Usually the many-body hamiltonian is approximated as a sum of one-body potentials, as it is in Hartree Fock and density functional theory, and in the quasiparticle self-consistent GW approximation, though they can be many-body in nature as well. A one-body potential is static and hermitian, which means the poles of the Green’s function are sharp δ-functions in energy and eigenstates are discrete. This continues to be true in extended systems; however, the crystal momentum k is a continuously varying quantum number (Bloch’s theorem), and the eigenstates (aka energy bands) are continuous functions of k. In general a one-body potential is nonlocal, meaning that the potential is orbital dependent. Nonlocality can also be expressed in as a potential of two spatial variables, $V(\mathbf{r},\mathbf{r}')$: since $\mathbf{r}$ and $\mathbf{r}'$ act on different wave functions when making matrix elements, e.g. $\langle\phi(\mathbf{r})\lvert{}V(\mathbf{r},\mathbf{r}')\rvert\phi(\mathbf{r}')\rangle$. Density-functional theory (DFT) (in its pure form, that is strictly a functional of the density and the same for all electrons) makes a local or semilocal approximation to the one-body potential, and it is a function of one variable, $V(\mathbf{r})$.

An essential feature of one-body theory is self-consistency: one-body potentials are made self-consistent, meaning that independent variable that generates the potential is iterated until it becomes equal the potential generates as output. The independent variable is the density in density-functional theory, wave functions in Hartree Fock theory, and Green’s function in QSGW.

Many body approaches

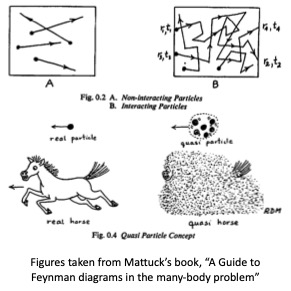
It is not possible to cast the many-electron problem exactly as a superposition of one-body potentials. It would seem unrealistic that a one-body potential can be reasonable at all, since the two-body electron-electron interaction is proportional to $e^2$, which is large ($e^2/a_0=27.2$ eV). Nevertheless one-body potentials can do a remarkably good job at predicting energy states. Angular-resolved photoemission (ARPES) experiments yield energy-distribution curves, which provide experimental evidence of the energy bands from the peaks in the spectra. The extent to which peaks are broadened out is a measure of correlation not captured by an independent-particle approximation. Different kinds of one-body approximations yield different energy bands, and one measure of the quality of a one-body approximation is its ability to reproduce ARPES.

Many-body theory no longer makes the independent particle approximation. Mattuck’s book very nicely depicts the difference between the two. In the top figures, independent particles do not interact, but evolve under some effect potential $V$ without scattering. Interactions cause the particles to scatter (top right figure). If the deviation from the one-body picture is not too large, electron are said to be “quasiparticles”, meaning that they are not pure electrons but get dressed by a “cloud,” as depicted in the bottom figures shown above. Most many-body approaches then correct some starting one-body part by adding interactions. Methods to incorporate interactions generally come in two classes: either they are functionals of the one-body wave functions they are quantum chemical methods. Alternatively they can be a functional of the one-body Green’s function. The two kinds of approaches are very different in character, though the are solving the same equation and there is a lot of overlap between the two. Questaal follows the Green’s function route.

It is still possible to construct a one-body Green’s function $G(\mathbf{r},\mathbf{r}',\omega)$, in the many-body case. The potential is now frequency- (or time-) dependent $V(\mathbf{r},\mathbf{r}',\omega)$, and is non-hermitian, with the non-hermitian part a measure of how long-lived the quasiparticle survives. The many-body part of $V$ is usually separated from the one-body part and is called the “self-energy” $\Sigma(\mathbf{r},\mathbf{r}',\omega)$. Many-body perturbation theory usually starts from a one-body hamiltonian and interactions are expressed in Feynman diagrams, each diagram representing one possible scattering path. The big achievement of many-body perturbation theory was to recognize that by far the largest many-body effect is the screening of the electron cloud. By making the diagrammatic series in the screened coulomb interaction $W$, Hedin [14] set the framework for modern Green’s function theory. Each diagram involves combinations of the Green’s function $G$ (a Fermion) and the screened coulomb interaction $W$ (a boson) that corresponds to a particular scattering sequence. The lowest order diagram makes $W$, calculated in the random phase approximation. Then $\Sigma= iGW$, which is why Hedin called it the “GW approximation.” GW was designed for excitations and response functions, though it has a corresponding total energy from the Luttinger-Ward functional. That is, derivatives of this functional with respect to $G$ yields the potential that generates $G$. The first implementation of the RPA total energy in a solid was coded in Questaal’s antecedent [15] but basis set incompleteness issues kept it from being a practical tool in Questaal. RPA total energy has been since developed in plane wave codes, and is now feasible. However the calculations are very inefficient because an enormous plane wave basis set is required to converge it reliably. Calculating total energy with basis set corrections is now an active area of development in Questaal, and we expect it to be available soon.

Dynamical mean field theory (DMFT) is another form of Green’s function theory. It is non-perturbative theory, but it includes only local diagrams for the interacting part, and embeds it in a one-body host. More precisely, DMFT is site-local but is nonlocal in the basis of some orbitals at a site. Usually these are the family orbitals of some $m$ quantum belonging to the same $\ell$, expressed in spherical harmonics. (usually the d or f orbitals); thus $\Sigma$ takes the form $\Sigma_{m,m'}(\omega)$. Usually only diagonal elements $\Sigma_{m,m}(\omega)$ are kept, owing to a severe sign problem that occurs if the full matrix structure is kept.

Relative merits of different approximations

Hartree-Fock theory is generally very poor in extended systems. It is used as a starting point for higher order approximations in quantum-chemical methods, where the wave function acts as the independent variable. One important advantage is that the theory is well posed: what is left in and what is omitted is well defined.

DFT is more accurate than Hartree Fock, and simpler. It is a ground state theory suitable for total energy and derivatives (e.g. forces), but the Lagrange multipliers that emerge from a Kohn-Sham construction are commonly interpreted as excitation energies, even though there is no formal basis for it. (DFT is almost always implemented by K-S construction.) For excited states, DFT has many well-known problems, and for that reason a vast number of ad-hoc corrections designed to handle one shortcoming or another have arisen over the years. Among the popular ones are DFT+U, or some blend of Hartree Fock and DFT character (called hybrid functionals) which can yield much better band structures. This is because the errors generated by the HF and DFT approximations are typically opposite in sign, and better results can be obtained by taking some mixture of them. The total energy of correlated materials is usually poor in DFT, and ad-hoc corrections to that shortcoming, such as DFT+U, or van der Waals corrections, have been also formulated for the total energy as well. DFT is by far the most popular approach to electronic structure, with well in excess of 10,000 papers published each year using it, because of its simplicity and ability to access larger systems.

Quantum-chemical methods are the king for accuracy. Its drawbacks are its high cost (for the high-fidelity methods) and poor scaling with system size. Also they are designed only for the ground state. Total energy is the most common quantity sought in quantum chemistry, so these methods have long been the method of choice when seeking high fidelity results in molecular systems. Questaal does not implement quantum chemical methods, and we do not attempt to address here the vast literature in these methods.

In the first ab initio formulation of many-body perturbation theory, $G$ and $W$ were constructed from the local density approximation to DFT, thus using it as starting point and the self-energy $\Sigma=iGW$ is a perturbative correction to the LDA exchange-correlation potential. This milestone work [15] continues to be the way most $GW$ calculations are carried out today, though other starting points are used. Such an approach is obviously starting-point dependent, which has an important consequence: benchmarks to establish the validity of the GW approximation become hazy, akin to ad hoc methods such as DFT+U. QSGW is a form of GW where the starting point is determined by GW itself, and is, by construction, which eliminates the ambiguity in the starting point .

The QSGW potential has a Hartree Fock structure, $V(\mathbf{r},\mathbf{r}')$. In QSGW $V(\mathbf{r},\mathbf{r}')$, is determined by GW itself, which it does by reifying a dynamical $\Sigma(\mathbf{r},\mathbf{r}',\omega)$ into an independent particle potential $\Sigma^0(\mathbf{r},\mathbf{r}')$ which plays the role of $V(\mathbf{r},\mathbf{r}')$. QSGW is self-consistent, but self-consistency in this context is designed to render the noninteracting $G_0$ to be as close to $G$ as possible. Ismail-Beigi [13] showed that $G_0$ satisfies a variational principle, though not the usual one. Thus QSGW is, by construction, is designed to be an optimum one-body potential, and as a result the errors in the theory can be identified unambiguously. QSGW is not perfect, but errors that do appear become much more systematic and uniform. Thus the theory is systematically improvable, since the systematics of the errors points to what is missing from the theory and needs to be added, in contrast to the patchwork of ad-hoc corrections to DFT, or GW based on an ad hoc starting point such as DFT. Perhaps the best illustration of this is the inclusion of ladder diagrams when constructing the screened coulomb interaction W [12]. This work establishes that the dominant error in QSGW occurs because of the RPA approximation to screening is a little too rough. Other important missing diagrams can also be identified: two of the dominant ones are diagrams for spin fluctuations, and a diagram for the electron-phonon interaction. In summary QSGW constructs two Green’s functions, $G$ and $G_0$, designed to be as similar to each other as possible. It can be shown that the poles of the two are same, meaning that the band structure in $G_0$ can be properly interpreted as excitation energies.

DMFT is a site-local theory and its strength lies in describing strong local correlations. It can be used in its own right, with a model hamiltonian as a reference. In an ab initio context, DMFT is usually combined with DFT. However, as in the MBPT case, the result depends on the fidelity of the reference, and when DMFT is combined with DFT, systematic errors appear. QSGW provides a much better starting point, so when DMFT is combined with it, the result is particularly powerful. QSGW’s handles charge fluctuations quite well, but primary failing comes its missing diagram for spin fluctuations. Spin fluctuations are low-energy and mostly local (more precisely the vertex generating them is mostly local), and they are what DMFT is particularly good at. So when QSGW and DMFT are taken together the fidelity is particularly high.

Executable codes in the Questaal suite

The executables in the Questaal suite a listed in the next section. They have potentials with the following form:

• lmf: $V=V(\mathbf{r})$ except when a QSGW potential is read in. Then $V=V(\mathbf{r},\mathbf{r}')$.
• lmgw.sh: Generates a dynamical self-energy $\Sigma(\mathbf{r},\mathbf{r}',\omega)$, but usually quasiparticlizes it to make $V=\Sigma^0(\mathbf{r},\mathbf{r}')$.
  There is a special mode that makes the dynamical sigma, to be postprocessed by lmfgws
• lmfgws: Operates on a dynamical self-energy $\Sigma(\mathbf{r},\mathbf{r}',\omega)$
• lmdmft: Makes nonlocal $\Sigma_{mm'}(\omega)$, site nonlocal in the $m,m'$ basis. $m$ and $m;$ are orbital with particular azimuthal quantum number belonging to the same $\ell$ on a site.
• lmgf: is a DFT code and $V=V(\mathbf{r})$. However, in CPA mode, $V=V(\mathbf{r,\omega})$.
• lmpg: same as lmgf

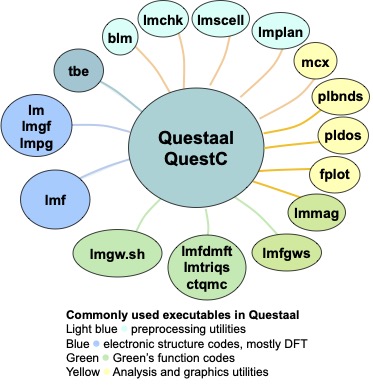
The Questaal family consists of a large variety of executables, including some DFT or beyond-DFT implementations of electronic structure, some postprocessing tools and some other utilities. The figure shows the most commonly used ones.

The beyond DFT Green’s function methods (GW and DMFT) work via interfaces connecting them and the main DFT code lmf. The DMFT solvers themselves are not contained in Questaal, but must be compiled separately.

This page organizes the features or properties accessible in Questaal, and what codes run them and tests or tutorials illustrate them.

Input for Questaal codes

Most of the executable programs that implement electronic structure or run preprocessing steps (blue and green ovals in the figure) share a common, elegant input system. These executables read from the same input file, ctrl.ext. The ctrl.ext file reader is a unique system that parses input in a largely format-free, tree-structured format. The ctrl files is initially read through a preprocessor with programming language capability: lines can be conditionally read, you can declare variables and use algebraic expressions. Thus the input file can be quite simple as it is in this introductory tutorial, or very detailed, even serving as a database for many materials. This page and this tutorial explain how an input file is structured, and how input is organized by categories and tokens. There is a reference manual that defines the syntax of categories and tokens that make up ctrl.ext. blm can generate this file from structural information.

Utilities to prepare input

• blm: an input file generator, given structural information. Many of the tutorials use blm.

• cif2init and cif2site: convert structural information contained in cif files to a form readable by Questaal. These codes read output from a translator cif2cell that converts a raw CIF (Crystallographic Information Framework) files into a simpler format. You must install cif2cell separately. poscar2init and poscar2site: perform a similar function, reading VASP POSCAR files. For an illustration, see this tutorial. site2init generates a Questaal init file blm reads from a Questaal site file.

• lmchk: performs numerous functions related to crystal structure, including making neighbor tables and bond angles, and checking augmentation sphere overlaps. There is an option to automatically determine sphere radii, and another option to locate interstitial sites where empty spheres or floating orbitals may be placed. This can be important when codes that make the Atomic Spheres Approximation (ASA) are applied to systems that are not fairly closed packed. In the full-potential context in open systems, sometimes the basis needs to be slightly enhanced for accurate GW calculations. See this tutorial and this tutorial for the basics, and this one for an advanced application. In the full potential context, this page provides an additional discussion. This tutorial uses them in the study of a heterojunction.

• lmscell: a supercell maker. It has two main branches: making supercells and superlattices. It is documented on this page. It has a special mode designed to inspect and manipulate the structure of layered systems lmscell --stack.

• lmplan: is an analyzer to inspect and manipulate the geometries of layered systems. Many of its functions have been superseded by lmscell --stack.

• rdcmd: a command reader, similar to a shell, but uses Questaal’s parser and programming language.

• lmxbs: generates input for the graphics program xbs written by M. Methfessel, which draws pictures of crystals.

One-body Electronic Structure Codes

• lmf: the standard full-potential DFT band program. This section describes other executables that are part of this suite. See also this page for a basic tutorial.

• lm: a density functional band program based on the Atomic Spheres Approximation (ASA). It requires a companion program lmstr to make structure constants for it. A basic tutorial can be found here.

• lmgf: a density functional Green’s function code based on the ASA. Its unique contribution to the suite is that it permits the calculation of magnetic exchange interactions, and has an implementation of the coherent potential approximation to treat chemical and/or spin disorder. A tutorial can be found here.

• lmpg: a program similar to lmgf, but it is designed for layered structures with periodic boundary conditions in two dimensions. It can calculate transport using the Landauer-Buttiker formalism, and has a non-equilibrium capability. It is documented in more detail here; a tutorial can be found here.

• tbe: an efficient band structure program that uses empirical tight-binding hamiltonians. One unique feature of this package is that self-consistent calculations can be done (important for polar compounds), and includes Hubbard parameters. It is also highly parallelized, and versions can be built that work with GPU’s. A path integrals formulation to account for quantum nuclear motion has been implemented. tbe has a tutorial.

• lmmc: a (fast) LDA-based molecules program (not documented).

Greens function implementations

• lmgw.sh is a script that performs QSGW calculations. The many-body part is run as a sequences of smaller executables (that generate the exchange potential, polarization operator, correlation potential, etc.), and they synchronize with lmf, which manages the one-body part. lmfgwd is a driver that generates information for the GW part. properties related to GW. The interface connecting to the GW code is lmfgwd. A further description of how to make lmgw.sh in an HPC environment is given in this tutorial. A basic tutorial for the GW package can be found on this web page.

• lmfdmft is an interface to the DMFT solvers. It can generate information needed by the DMFT solver, and reads information generated by it to perform various other functions. The DMFT code is not part of Questaal and must be installed separately. The steps to run DMFT are explained in this tutorial. The process is a bit complicated, however and the tutorial has not been updated for some time.

• lmfgws: analyses spectral functions of interacting hamiltonians. It is run a post-processing utility after a GW or DMFT (but not CPA) calculation. It is used in this tutorial.

Supporting or Postprocessing codes

• lmdos: generates partial densities of states. It is run as a post-processing step after execution of lmf, lm, or tbe. This tutorial illustrates several contexts for which lmdos can be used.

• fplot is a graphics utility, with many functionalities similar to gnuplot.

• plbnds: is a utility reads energy band data generated by lmf, lm, or tbe, or spectral function data generated by lmfgws. plbnds reformat the data into files suitable for further processing, and can generate a script for fplot or gnulot.

• pldos: is a utility that reads partial density-of-states generated usually by lmdos, and organizes the data into files suitable for further processing, e.g. a script for fplot.

• bandedge: is a script that aids in finding maxima or minima of a band, or determine effective masses. Its operation is explained in this tutorial.

• spectral: takes the raw output of the GW dynamical self-energy generator and renders a file in the se format that lmfgws can read. It is used in this tutorial.

• s2s5: Translates a binary QSGW self-energy file which lmf reads, to an hdf5 format, used by the GW package.

• mcx: is a matrix calculator.

• pfit: is a least square fitting program (not documented)

• dval: is a calculator (not documented)

• map-results-irr-to-fbz: A utility, used after a magnetic susceptibility calculation, to generate magnetic exchange interactions

A number editors are embedded in these codes that provide additional functionality, e.g. manipulate restart files, self-energy files, or structural information.

Other Resources

1. This is the main paper describing Questaal’s features. Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).

2. This book chapter describes the theory of the lmf code. It is a bit dated but the basics are unchanged. M. Methfessel, M. van Schilfgaarde, and R. A. Casali, ``A full-potential LMTO method based on smooth Hankel functions,’’ in Electronic Structure and Physical Properties of Solids: The Uses of the LMTO Method, Lecture Notes in Physics, 535, 114-147. H. Dreysse, ed. (Springer-Verlag, Berlin) 2000.

3. The mathematics of smoothed Hankel functions that form the lmf basis set are described in this paper: E. Bott, M. Methfessel, W. Krabs, and P. C. Schmid, Nonsingular Hankel functions as a new basis for electronic structure calculations, J. Math. Phys. 39, 3393 (1998)

4. This classic paper established the framework for linear methods in band theory: O. K. Andersen, “Linear methods in band theory,” Phys. Rev. B12, 3060 (1975)

5. This paper lays out the framework for screening the LMTO basis into a tight-binding form: O. K. Andersen and O. Jepsen, “Explicit, First-Principles Tight-Binding Theory,” Phys. Rev. Lett. 53, 2571 (1984)

6. This paper explains how LAPW and generalized LMTO methods can be joined: T. Kotani and M. van Schilfgaarde, A fusion of the LAPW and the LMTO methods: the augmented plane wave plus muffin-tin orbital (PMT) method, Phys. Rev. B81, 125117 (2010)

7. This paper presented the first description of an all-electron GW implementation in a mixed basis set: T. Kotani and M. van Schilfgaarde, All-electron GW approximation with the mixed basis expansion based on the full-potential LMTO method, Sol. State Comm. 121, 461 (2002).

8. These papers established the framework for QuasiParticle Self-Consistent GW theory: Sergey V. Faleev, Mark van Schilfgaarde, Takao Kotani, All-electron self-consistent _GW approximation: Application to Si, MnO, and NiO_, Phys. Rev. Lett. 93, 126406 (2004); M. van Schilfgaarde, Takao Kotani, S. V. Faleev, Quasiparticle self-consistent GW theory, Phys. Rev. Lett. 96, 226402 (2006)

9. Questaal’s GW implementation is based on this paper: Takao Kotani, M. van Schilfgaarde, S. V. Faleev, Quasiparticle self-consistent GW method: a basis for the independent-particle approximation, Phys. Rev. B76, 165106 (2007)

10. This paper shows results from LDA-based GW, and its limitations: M. van Schilfgaarde, Takao Kotani, S. V. Faleev, Adequacy of Approximations in GW Theory, Phys. Rev. B74, 245125 (2006)

11. This book explains the ASA-Green’s function formalism, including the coherent potential approximation: I. Turek et al., Electronic structure of disordered alloys, surfaces and interfaces (Kluwer, Boston, 1996).

12. Brian Cunningham, Myrta Gruening, Dimitar Pashov, Mark van Schilfgaarde, QSGW: Quasiparticle Self consistent GW with ladder diagrams in W, Phys. Rev. B 108, 165104 (2023)

13. Sohrab Ismail-Beigi “Justifying quasiparticle self-consistent schemes via gradient optimization in Baym–Kadanoff theory,” J. Phys.: Condens. Matter 29 385501 (2017).

14. L. Hedin, New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem, Phys. Rev. 139, A796 (1965).

15. T. Miyake, F. Aryasetiawan, T. Kotani, M van Schilfgaarde, M. Usuda, K. Terakura, Total energy of solids: an exchange- and random-phase approximation correlation study, Phys. Rev. 66, 245103 (2002).

16. Mark S. Hybertsen and Steven G. Louie, Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies, Phys. Rev. B 34, 5390 (1986).